On dit souvent que le temps coule comme une rivière. Chaque seconde suit la précédente, chaque minute se déroule de manière régulière, comme les perles d’un collier. Cette image rassure : elle nous donne l’impression que nous avançons tous ensemble sur un même fil continu.
Pourtant, la physique moderne a fissuré cette évidence. Einstein a montré qu’il n’existe pas de temps absolu : deux horloges qui suivent des trajets différents ne se retrouvent pas parfaitement synchronisées. Le temps reste linéaire localement, pour chaque observateur, mais il peut se décaler globalement selon les parcours.
À partir de là, pourquoi ne pas aller plus loin ? Pourquoi ne pas imaginer que le temps n’est pas une simple ligne, mais une variété beaucoup plus riche ?
Une dimension par quantum de Planck
Le plus petit « grain de temps » que la physique conçoit est le temps de Planck : environ 10−44 secondes. Depuis le Big Bang, il s’en est écoulé près de 1060.
Imaginons alors une construction audacieuse : et si chacun de ces 1060 quanta n’était pas seulement une « unité » qui s’empile sur les autres, mais une dimension propre ?
Le temps ne serait plus une ligne, mais un espace hyperdimensionnel gigantesque. Notre vécu linéaire du temps — le temps qui « coule » seconde après seconde — ne serait que la projection d’un trajet beaucoup plus complexe dans cet espace.
Localement linéaire, globalement mouvant
Dans ce modèle, la perception que nous avons d’un présent qui « file » régulièrement correspond au temps local : une coupe linéaire dans l’espace hyperdimensionnel. Mais globalement, il peut exister des détours, des enroulements, des holonomies temporelles.
C’est un peu comme marcher sur un escalier en colimaçon :
-
à chaque pas, on croit avancer tout droit ;
-
mais quand on prend du recul, on voit qu’on a en fait gravi un étage.
De la même manière, chacun de nous suit sa propre spirale de présent, invisible au pas-à-pas mais manifeste dans le vécu global.
Chacun vit sa propre vie
Cette hypothèse éclaire notre intuition humaine profonde : pourquoi avons-nous tous l’impression de vivre des vies si différentes, avec nos rythmes, nos accélérations, nos lenteurs ?
Parce que, dans cet espace hyperdimensionnel du temps, chacun trace sa propre coupe. Nous partageons la même origine cosmique — le Big Bang — mais nos présents se déploient différemment, en fonction des chemins que nous prenons, des choix que nous faisons, des intensités que nous vivons.
Le plus-que-présent
C’est une définition de plus du plus-que-présent :
-
localement, le présent semble couler comme une ligne droite ;
-
globalement, il s’enroule, se déploie, se dédouble, selon la trajectoire que nous traçons dans l’hyper-espace du temps.
Le plus-que-présent, c’est cette conscience que nos instants ne sont pas seulement une succession mécanique, mais les reflets d’une structure plus profonde, où le temps est multiple et singulier à la fois.
> On peut donc accepter que le temps n’est pas un fleuve unique, mais une forêt de directions invisibles, dont chacun de nous explore un sentier différent ?
Annexe mathématique : Esquisse d’une structure du temps hyperdimensionnel
On part de deux postulats :
-
Localement, le temps est linéaire : il ressemble à une ligne où chaque pas est régulier (comme en relativité).
-
Globalement, le temps peut s’enrouler : son parcours dépend du chemin suivi dans un espace plus grand.
L’espace des présents
Soit le nombre de temps de Planck depuis le Big Bang :
\(
N \approx 10^{60}
\)
On associe à chaque quantum de temps une coordonnée \(t_i\).
L’« espace du temps » devient alors :
\(
\mathcal{T} = \mathbb{R}^{N}
\)
un espace de très haute dimension.
Le présent vécu comme une projection
Un observateur ne peut pas parcourir toutes les dimensions à la fois. Son temps perçu est une projection linéaire :
\(
T(\tau) = \sum_{i=1}^{N} v_i(\tau), t_i
\)
où \(\tau\) est le paramètre propre (le temps « interne » de l’observateur), et \(v_i(\tau)\) représente la « direction » suivie dans la dimension \(t_i\).
Localement linéaire
Sur un petit intervalle, la dérivée est régulière :
\(
\frac{dT}{d\tau} = \text{constante}
\)
> Cela correspond à notre impression que le temps « coule » normalement.
Globalement enroulé
Si on fait un parcours fermé dans \(\mathcal{T}\), on peut accumuler une dérive :
\(
\Delta T = \oint_{\gamma} \alpha
\)
où \(\alpha\) est une 1-forme temporelle définissant la « connexion » entre les dimensions.
> Comme dans la relativité, deux observateurs qui suivent des chemins différents peuvent se retrouver désynchronisés, mais ici le décalage dépend de la topologie de l’hyper-espace temporel.
Image intuitive
Localement :
\(
dt = d\tau
\)
tout est linéaire.
Globalement : le temps est comme un escalier en colimaçon — chaque pas est horizontal, mais au bout d’un tour, on a pris de la hauteur.
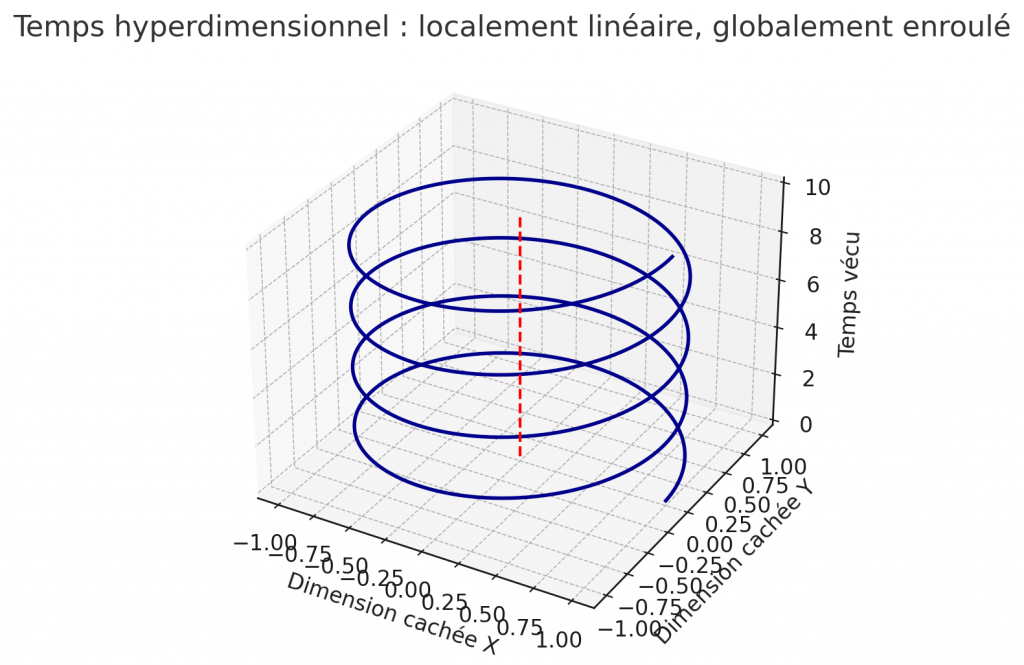
La ligne rouge en pointillés représente le temps classique, perçu comme une flèche unique. La spirale bleue illustre le temps hyperdimensionnel : localement, chaque pas est linéaire, mais globalement, le présent peut s’enrouler et produire un décalage.

